Answer:
337.5m
Step-by-step explanation:
Kinematics
Under constant acceleration, the kinematic equation holds:
 , where "s" is the position at time "t", "a" is the constant acceleration, "
, where "s" is the position at time "t", "a" is the constant acceleration, "
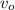 " is the initial velocity, and
" is the initial velocity, and
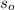 is the initial position.
is the initial position.
Defining Displacement
Displacement is the difference in positions:
 or
or


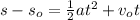
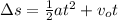
Using known information
Given that the initial velocity is zero ("skier stands at rest"), and zero times anything is zero, and zero plus anything remains unchanged, the equation simplifies further to the following:
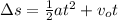

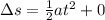
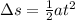
So, to find the displacement after 15 seconds, with a constant acceleration of 3.0 m/s², substitute the known values, and simplify:
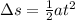
![\Delta s=(1)/(2)(3.0[(m)/(s^2)])(15.0[s])^2](https://img.qammunity.org/2023/formulas/physics/high-school/l6zxv30w5qc177r2372lphbqir7qzoyeae.png)
![\Delta s=337.5[m]](https://img.qammunity.org/2023/formulas/physics/high-school/p88nhj1y68dxhd3hxuwiekw74ev7np6fxf.png)