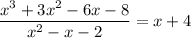Answer:
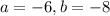
Remaining factor =
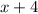
Explanation:
Given that:
Two polynomials:
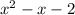 and
and

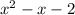 is a factor of
is a factor of
 .
.
To find:
The values of
 and
and
 from the cubic equation and the remaining factor.
from the cubic equation and the remaining factor.
Solution:
Let us first of all, factorize
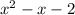 .
.
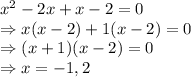
There are two factors of the given quadratic equation.
These two factors must also be factors of the cubic equation as well.
Putting
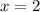 :
:
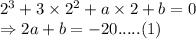
Putting
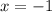 :
:
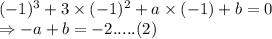
Subtracting (2) from (1):

From equation (1):
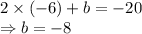
Putting the values of
 and
and
 in the cubic equation, we get:
in the cubic equation, we get:

Dividing the cubic equation with quadratic, we get: