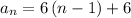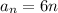Question

The sum of the first (n) terms of the sequence is given by the formula (given below) . If this sequence is a geometric progression, find q. If this sequence is an Arithmetic progression, find d​

Answer 1

We have established the following sequence

6, 12, 18,...

The given is the Arithmetic sequence with the nth term

`a_n=6n`

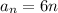
d = 6 is a common difference.

Explanation:

Given the formula

Sₙ = 3n² + 3n

Put n = 1 to determine the sum of the first term

S₁ = 3(1)² + 3(1)

S₁ = 3 + 3

S₁ = 6

As the sum of the first term includes the only first term, so

a₁ = 6

Put n = 2 to determine the sum of the two terms

Sₙ = 3n² + 3n

S₂ = 3n² + 3n

S₂ = 3(2)² + 3(2)

S₂ = 12 + 6

S₂ = 18

as

S₂ = a₁ + a₂

substituting S₂ = 18, a₁ = 6

18 = 6 + a₂

12 = a₂

so

a₂ = 12

Put n = 3 to determine the sum of the two terms

Sₙ = 3n² + 3n

S₃ = 3(3)² + 3(3)

S₃ = 27 + 9

S₃ =36

as

S₃ = a₁ + a₂ + a₃

substitutingS₃ =36, a₁ = 6, a₂ = 12

36 = 6+12+a₃

a₃ = 36-6-12

a₃ = 18

Thus,

a₁ = 6

a₂ = 12

a₃ = 18

Therefore, the sequence becomes

a₁, a₂, a₃,...

6, 12, 18,...

Let us check the common difference 'd' between the adjacent terms

d = 12 - 6 = 6

d = 18 - 12 = 6

As the common difference 'd' between adjacent terms is the same, therefore the sequence is Arithmetic.

Thus,

• d = 6

Furthermore, the nth term of the Arithmetic sequence can be defined as

`a_n=a_1+\left(n-1\right)d`

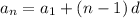
substituting d = 6 and a₁ = 6

`a_n=6\left(n-1\right)+6`

`a_n=6n`