Answer:
True
Explanation:
Given
In JKL, we have:
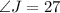
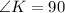
In WXY, we have:
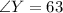
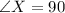
Required
Is JKL ~ WXY?
In both triangles, we already have one similar angle (90)
Next, is to determine the third angles in both triangles.
In JKL
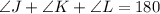
We have that:
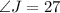 and
and
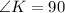
The expression becomes:
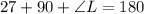
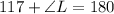
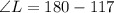
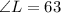
In WXY
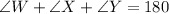
We have that:
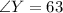 and
and
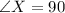
The expression becomes:
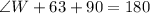
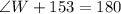
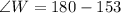
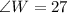
The three angles in JKL are:
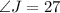
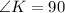
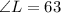
The three angles in WXY are:
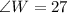
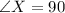
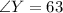
By comparing the angles, we can conclude that both triangles are similar because of AAA postulate (Angle-Angle-Angle)