Question

The MagicSoft software company has a proposal to the city council of Alva, Florida, to relocate there. The proposal claims that the company will generate $3.3 million for the local economy by the $1 million in salaries that will be paid. The city council estimates that 70% of the salaries will be spent in the local community and 70% of that money will again be spent in the community, and so on. What is the correct estimate of the amount generated to the local economy?

Answer 1

it A

Explanation:

Answer 2

The correct estimate of the amount generated to the local economy is $3,333,333.
`\bar3`

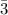
Explanation:

The amount the expected to be generated for the local economy = $3.3 million

The amount of salaries that will generate $3.3 million = $1 million

The percentage of the amount of the salaries and the subsequent earnings expected to be spent on the local community = 70%

Therefore, we have;

For a first amount of 1 million into the economy, the next amount to into the economy is 70/100 × 1 million = 700,000, then we have 70/100 × 700,000 and so on, which is a geometric sequence, with first term, a = $1 million, the common ratio, r = 70/100 = 0.7, the number of terms = Infinity = ∞

The sum of a geometric sequence to infinity is given as follows;

`\sum\limits_(k = 0)^(\infty )a \cdot r^k = S_(\infty) = (a)/(1 - r)`

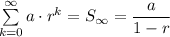
Substituting the known values gives;

`\sum\limits_(k = 0)^(\infty )1,000,000 * 0.7 ^k = (1,000,000)/(1 - 0.7)= 3,333,333.\bar 3`

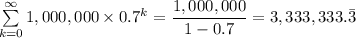
Therefore, the correct estimate of the amount generated to the local economy by the $1 million salaries that will be paid = $3,333,333.
`\bar3`.