Question

The radius of a spare whose surface area is 17 whole one over nine​

Answer 1

`r = (7)/(6)`

Step-by-step explanation:

Given

Shape: Sphere

`Surface\ Area = 17(1)/(9)`

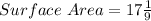
Required

Determine the radius (r)

A sphere's surface area of is calculated using:

`Surface\ Area = 4\pi r^2`

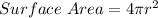
Substitute value for Surface Area

`17(1)/(9) = 4\pi r^2`

Convert fraction to improper number

`(154)/(9) = 4\pi r^2`

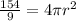
Divide both sides by 4

`(154)/(9*4) = \pi r^2`

`(77)/(9*2) = \pi r^2`

`(77)/(18) = \pi r^2`

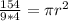
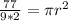
Divide both sides by
`\pi`

`(77)/(18) * (1)/(\pi) = r^2`

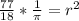
Take
`\pi` as
`(22)/(7)`

So, we have:

`r^2 = (77)/(18) * (7)/(22)`

`r^2 = (7)/(18) * (7)/(2)`

`r^2 = (49)/(36)`

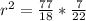
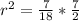
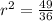
Take the square root of both sides

`r = \sqrt{(49)/(36)}`

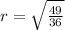
`r = (7)/(6)` --- approximated

Hence, the radius of the sphere is 7/6 units