Question

9. The diameter of the Earth is 7899.83 miles from the North Pole to the South Pole and 7926.41 miles from opposite points at the equator.

a. Find the approximate surface area of Earth using each measure.
b. About 75% of Earth's surface is covered by water. Find the surface area of water on Earth, using the diameter of the Earth is 7926.41 miles from opposite points at the equator.​

Answer 1

a. The approximate surface area of the Earth based on the diameter of the Earth measured from the poles is approximately 1.961 × 10⁸ mi²

The approximate surface area of the Earth based on the diameter of the Earth measured from the equator is approximately 1.974 × 10⁸ mi²

b. The surface area of the water on Earth using the diameter of the Earth measured from opposite points of the equator is approximately 1.480 × 10⁸ mi²

Explanation:

The given parameters are;

The diameter of the Earth measured from the North to the South pole,
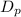`D_p` = 7899.83 miles

The diameter of the Earth measured from (across) opposite points of the equator,
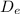`D_e` = 7926.41 miles

a. The surface area,
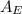`A_E`, of the Earth, taking the Earth as a perfect sphere, is given as follows;

A = 4 × π × r²

Where;

r = The radius of the sphere = 1/2 × the diameter of the sphere

For the diameter measured from poles,
`r_p` =
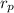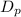`D_p`/2 = (7899.83 miles)/2 = 3949.915 miles

The approximate surface area of the Earth based on the diameter of the Earth measured from the poles,
`A_(Ep)` = 4 × π × (3949.915 miles)² = 196058359.283 mi² ≈ 1.961 × 10⁸ mi²

For the diameter measured from equator,
`r_e` =
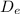`D_e`/2 = (7926.41 miles)/2 = 3963.205 miles

The approximate surface area of the Earth based on the diameter of the Earth measured from the equator,
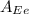`A_(Ee)` = 4 × π × (3963.205 miles)² = 197379906.233 mi² ≈ 1.974 × 10⁸ mi²

b. The percentage of the surface area of the Earth covered by water ≈ 75%

The surface area of water on Earth using the diameter of the Earth = 7926.41 miles (the diameter measured from the equator), we have;

The area of the Earth with a diameter of 7926.41 miles was given as
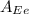`A_(Ee)` = 4 × π × ((7926.41 miles)/2)² = 197379906.233 mi²

The surface area of the water on Earth = 75% × The area of the Earth = 75/100 × 197379906.233 = 148034929.675 mi² ≈ 1.480 × 10⁸ mi²