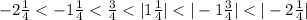Answer:
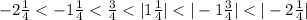
Explanation:
Given the numbers:
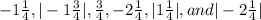
To find:
The ascending order of the given numbers.
Solution:
First of all, let us have a look at the definition of absolute value function i.e. Modulus function.
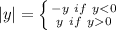
i.e. if the numbers is negative, then a negative sign is added to make the number positive.
Now, let us have a look at the given numbers with modulus one by one.
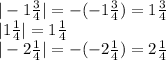
Smallest numbers are with negative signs.
And negative numbers with larger magnitude are smaller.
Therefore, the ascending order will be: