Answer:
Amplitude: 4
Period: 0.898 seconds.
Phase shift: 6.142 radians.
Step-by-step explanation:
A sinusoidal function is defined by the following model:
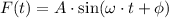 (1)
(1)
Where:
 - Amplitude.
- Amplitude.
 - Angular frequency, measured in radians per second.
- Angular frequency, measured in radians per second.
 - Phase shift, measured in radians.
- Phase shift, measured in radians.
We need to transform the given function into this form by trigonometric means. The following trigonometric identity is used:
 (2)
(2)
Then,
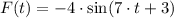
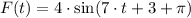
Then, the following information is found:
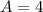 ,
,
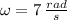 ,
,
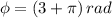
The period of the given function (
 ), measured in seconds, is determined by the following formula:
), measured in seconds, is determined by the following formula:
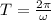 (3)
(3)
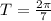
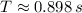
Then, the following information is found:
Amplitude: 4
Period: 0.898 seconds.
Phase shift: 6.142 radians.