Answer:
a) x = 14
b) The perimeter of △QRS is 77 units.
Explanation:
a) Due to the question asking for a solution using the Triangle Proportionality Theorem, it is assumed that △RQS is similar to the smaller triangle inside it.
Let us define the point at which the line inside △RQS meets line RQ as T, and the point at which that same line meets line RS as V.
Hence, △RTV ~ △RQS.
According to the Triangle Proportionality Theorem:
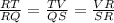
Hence, we can substitute all values that we know from the diagram:
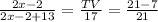
After getting this information, all we have to do is simplify and solve the equation:
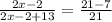
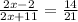
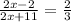
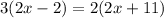
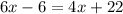

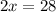
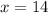
To verify this answer, we can plug in the value of x into the equation:
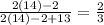
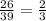

Hence, after verification, we can get the answer: x = 14.
--------------------------------------------------------------------------------------------------------------
b) To find the perimeter of △QRS, all we have to do is to add all the lengths of the sides of △QRS together.
Hence, 2(14) - 2 + 13 + 17 + 21
= 28 - 2 + 13 + 17 + 21
= 77 units
Therefore, the perimeter of △QRS is 77 units.
Hope this helped!