Answer:
The sum of the two vectors is 161.278 m.
Step-by-step explanation:
Given;
vector, B = 101 m inclined at angle 60⁰
vector, A = 85 m inclined at angle 0⁰
Y-component of the vectors;
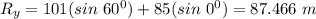
X-component of the vectors;
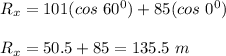
Sum of the two vectors;
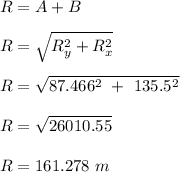
Therefore, the sum of the two vectors is 161.278 m.