Answer:
Question 3)

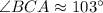
Question 1)

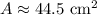
Explanation:
Question 3)
We are given that the central angle is 1.8 radians and has a radius of 20 inches.
Part A)
The formula for arc length in terms of radians is given by:
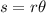
Where s is the arc length, r is the radius, and θ is the angle in radians.
In this case, r is 20 and θ is 1.8. Hence, the arc length is:
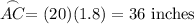
Part B)
∠BCA is the central angle that measures 1.8 radians.
We can convert radians to degrees using the following formula:
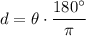
Where d is the measure in degrees, and θ is the measure in radians.
Therefore:
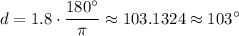
Question 1)*
Part A)
We will use the arc length formula in degrees given by:
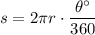
Where r is the radius and θ is the angle measured in degrees.
We have a radius of 10 centimeters and a central angle of 51°. Therefore, our arc length is:
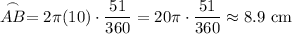
Part B)
We will use the formula for the area of a sector in degrees given by:
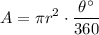
So, we will substitute 10 for r and 51 for θ. Hence, the area of the sector is:
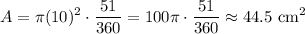
*Notes:
For this question, it is possible and completely fine for us to convert 51° to radians and then use the formulas in terms of radians.