Answer:
30.5 cm^2
Explanation:
General outline
- Find the area of the full circle
- Find the area of the rectangle
- Find the difference (full circle area - rectangle area)
Step 1. Find the area of the full circle
Recall the formula for the area of a circle:
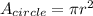 where
where
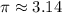 , and "r" is the radius of the circle (distance from center to any point on the edge).
, and "r" is the radius of the circle (distance from center to any point on the edge).
From the diagram, the radius is 5cm.
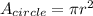
![A_(circle)=(3.14)(5[cm])^2](https://img.qammunity.org/2023/formulas/mathematics/college/hx8gb43bvzspsl1yj7spnda44aoxspxhc6.png)
![A_(circle)=78.5[cm^2]](https://img.qammunity.org/2023/formulas/mathematics/college/g18dmn47rrr1d8hny7eqe6gcskjfg5q30m.png)
Step 2. Find the area of the rectangle
Recall the formula for the area of a rectangle:
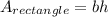 where "b" is the base of the rectangle (length of bottom or length of top), "h" is the height of the rectangle (distance from bottom to top).
where "b" is the base of the rectangle (length of bottom or length of top), "h" is the height of the rectangle (distance from bottom to top).
From the diagram, the base is 8cm, and the height is 6cm.
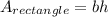
![A_(rectangle)=(8[cm])(6[cm])](https://img.qammunity.org/2023/formulas/mathematics/college/fvissfe14xkj08leksnwpxd0fd8l1q29ox.png)
![A_(rectangle)=48[cm^2]](https://img.qammunity.org/2023/formulas/mathematics/college/wnqqady7p5ev7m39mfrza4xtgbsvalo538.png)
Step 3. Find the difference (full circle area - rectangle area)
Having found the areas for each of the first parts, we can find the difference to find the shaded area:
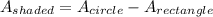
![A_(shaded)=(78.5[cm^2])-(48[cm^2])](https://img.qammunity.org/2023/formulas/mathematics/college/kd8f55fvu8pvjpuu3vd2l141gg6r1sfhad.png)
![A_(shaded)=30.5[cm^2]](https://img.qammunity.org/2023/formulas/mathematics/college/ws663rcdq7ofir8whez5yg83uy0t81bygp.png)