Question

the friction of water on a boat produces an acceleration of -10m/s^2. if the boat is traveling at 30 m/s and the motor shut off, how long does it take the boat to slow down to 5.0 m/s?

Answer 1

The boat takes 2.5 seconds to slow down to 5.0 m/s.

Step-by-step explanation:

The friction of water on a boat produces a negative acceleration of -10 m/s2. If the boat is traveling at 30 m/s and the motor shuts off, we can calculate the time it takes for the boat to slow down to 5.0 m/s using the equation:

vf = vo + at

Where:

• vf is the final velocity (5.0 m/s)
• vo is the initial velocity (30 m/s)
• a is the acceleration (-10 m/s2)
• t is the time taken

Substituting the given values into the equation, we get:

5.0 = 30 + (-10)t

Simplifying the equation, we find:

t = (30 - 5.0) / -10

t = 2.5 seconds

Therefore, it takes the boat 2.5 seconds to slow down to 5.0 m/s.

Answer 2

The boat takes 2.5 seconds to slow down to 5 m/s

Step-by-step explanation:

Motion With Constant Acceleration

It's a type of motion in which the velocity of an object changes uniformly in time. The equation that rules the change of velocities is:

`v_f=v_o+at\qquad\qquad [1]`

Where:

a = acceleration

vo = initial speed

vf = final speed

t = time

Using the equation [1] we can solve for a:

`\displaystyle a=(v_f-v_o)/(t)`

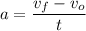
The acceleration produced by the friction of water is
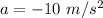`a=-10 \ m/s^2` and the boat is initially traveling at v0=30 m/s. When the motor is shut off, the boat will start braking until it stops. We need to find the time it takes to ready the final speed of vf=5 m/s.

Let's solve the above equation for t:

`\displaystyle t=(v_f-v_o)/(a)`

`\displaystyle t=(5-30)/(-10)`

`\displaystyle t=(-25)/(-10)`

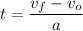
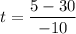
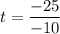
t = 2.5 s

The boat takes 2.5 seconds to slow down to 5 m/s