Answer:
The inverse of the function f(x) is h(x) = 4x + 48 ⇒ (D)
Explanation:
To find the inverse of a function do these steps
- Replace f(x) by y
- Switch x and y
- Solve to find the new y
- Replace y by
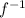 (x)
(x)
Let us do these steps to solve the equation
∵ f(x) =
 x - 12
x - 12
→ Replace f(x) by y
∴ y =
 x - 12
x - 12
→ Switch x and y
∴ x =
 y - 12
y - 12
→ Add 12 to both sides
∵ x + 12 =
 y - 12 + 12
y - 12 + 12
∴ x + 12 =
 y
y
→ Multiply each term by 4
∵ 4(x) + 4(12) = 4(
 y)
y)
∴ 4x + 48 = y
→ Switch the two sides
∴ y = 4x + 48
→ Replace y by h(x)
∴ h(x) = 4x + 48
∴ The inverse of the function f(x) is h(x) = 4x + 48