Answer:
The area of the square increases by 96%
Explanation:
Assume that the side of the square is x units
∵ The original side of the square = x
∵ The area of the square = side × side
∴ The original area of the square = x × x
∴ The original area of the square = x²
∵ The length of each side of a square increases by 40%
∴ The new side of the square = x + 40% × x
∴ The new side of the square = x +
× x
∴ The new side of the square = x + 0.4x
∴ The new side of the square = 1.4x
→ Find the area of the new square
∴ The new area of the square = 1.4x × 1.4x
∴ The new area of the square = 1.96x²
→ Find the increase in the area
∵ The increase of area = new area - original area
∴ The increase of area = 1.96x² - x²
∴ The increase of area = 0.96x²
∵ The percentage of the increase = (increase ÷ original) × 100%
∴ The percentage of the increase in the area =
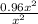× 100%
∴ The percentage of the increase in the area = 96%
∴ The area of the square increases by 96%