Question

Find the length of segments FD & FE? Show the work.

Answer 1

FD = 8

FE = 21.6

Explanation:

By applying Pythagoras theorem in ΔCDF,

CD² = CF² + FD²

(17)² = (15)² + FD²

289 = 225 + FD²

FD =
`√(289-225)`

=
`√(64)`

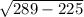
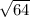
FD = 8 units

Since AB║DE and CD is a transversal line,

∠BCD ≅ ∠CDF [Alternate interior angles]

m∠CDF = m∠BCD = 55°

By using cosine rule in the right triangle CDE,

cos(55)° =
`\frac{\text{Adjacent side}}{\text{Hypotenuse}}` =
`(CD)/(DE)`

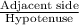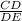
cos(55)° =
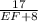
`(17)/(EF+8)`

EF + 8 =
`\frac{17}{\text{cos}(55)}`

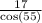
FE = 29.64 - 8

≈ 21.6 units