Answer:
70.45 kg.m^2/s
Step-by-step explanation:
Mass of the rod = M = 14.7 kg
Length of the rod = L = 2.85 m
Moment of inertia of the rod about one of its ends = I
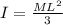

I = 82.369 kg.m^2
Angular speed of the rod = ω = 3.60 rad/s
Magnitude of the rod's angular momentum = L
L = Iω
L = (82.369)(3.60)
L = 70.45 kg.m^2/s
Magnitude of the rod's angular momentum = 70.45 kg.m^2/s