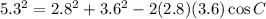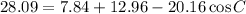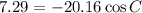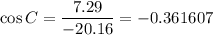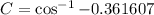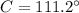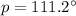Any help much appreciated:)

Question

asked Sep 8, 2021 85.2k views

1 Answer

Eric Lafortune · Answer 1 · 2021-09-12T16:56:33+0000

Answer:

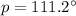
$p = 111.2^\circ$

Explanation:

Since you only have sides given, you must use the law of cosines.

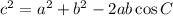
$c^2 = a^2 + b^2 - 2ab \cos C$

Let angle p be angle C in the law of cosines formula. Then a is 2.8 cm, b is 3.6 cm, and c is 5.3 cm.

All units of length are cm, so I'll leave them out for simplicity.

$5.3^2 = 2.8^2 + 3.6^2 - 2(2.8)(3.6) \cos C$

$28.09 = 7.84 + 12.96 - 20.16 \cos C$

$7.29 = -20.16 \cos C$

$\cos C = (7.29)/(-20.16) = -0.361607$

$C = \cos^(-1) -0.361607$

$C = 111.2^\circ$

$p = 111.2^\circ$