Question

Help a girl out haha

Answer 1

<A is 53.13 degrees

Explanation:

First find how long is side AB.

To do that, use the Pythagorean Theorem formula

`C = √(a^2 + b^2)`

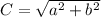
C is side AC

A is side AB

B is side BC

But we already know side AC and BC.

Side AC is 5

Side BC is 4

But we don't know side AB.

So instead use this formula

`A = √(c^2 - b^2)`

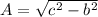
Now plug in the numbers and find side AB.

`3 = √(5^2 - 4^2)`

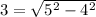
You will see that side AB is 3.

Now use cos-1(3.5) to find angle A and put in the calculator.

After putting it in the calculator, cos-1(3/5) equals 53.13 degrees

So the final answer for <A is 53.13 degrees

Hope it helped! My answer is expert verified.

Answer 2

We can use inverse sin to solve this

cos=adjacent/hypotenuse while sin=opposite/hypotenuse

therefore, cos(c)=sin(a)

if cos(c)=4/5 then BC=4 and AC =5

sin(a)=4/5

`sin^-1(0.8) =a\\`

using a calculator we get 53.13010235° or just 53°

Explanation: