Question

The volume of a certain right circular cylinder is 16. A larger circular cylinder has radius 25% greater and height 50% greater than the radius and height respectively, of the smaller cylinder. What is the volume of the larger cylinder

Answer 1

`V_2 = 37.5`

Explanation:

Given

`Volume = 16`

Represent the height of the smaller cylinder with h and its radius with r.

The height (H) of the larger cylinder is

`H = h + 50\% * h`

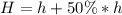
And the radius (R) is;

`R = r + 25\% * r`

Required

Determine the volume of the larger cylinder

Volume of the smaller cylinder is:

`V_1 = \pi r^2h`

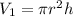
Substitute 16 for V1

`16 = \pi r^2h`

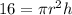
While the volume of the larger cylinder is:

`V_2 = \pi R^2H`

We have that:

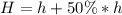`H = h + 50\% * h` and
`R = r + 25\% * r`

--------------------------------------------------------------------------------------------------------------

Simplify both expressions

`H = h + 50\% * h`

`H = h + 0.50*h`

`H = h + 0.50h`

`H = 1.50h`

`R = r + 25\% * r`

`R = r + 0.25*r`

`R = r + 0.25r`

`R = 1.25r`

--------------------------------------------------------------------------------------------------------------

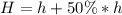
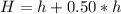
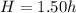
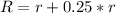
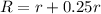
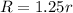
Substitute values for R and H in
`V_2 = \pi R^2H`

`V_2 = \pi * (1.25r)^2 * 1.50h`

`V_2 = \pi * 1.5625r^2 * 1.50h`

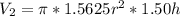
Collect Like Terms

`V_2 = 1.50 * 1.5625* \pi*r^2 * h`

`V_2 = 2.34375* \pi*r^2 * h`

`V_2 = 2.34375* \pi r^2h`

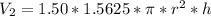
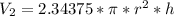
Recall that:
`16 = \pi r^2h`

`V_2 = 2.34375* 16`

`V_2 = 37.5`

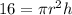
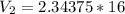
Hence, the volume of the larger cylinder is 37.5