Question

Solve -4x² = 5x + 9. *a x=-1 or x=-1/4 x=-1 or x = 9/4 x= 2 or x= 3 No real solutions

Answer 1

No real solutions

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

Algebra I

• Standard Form: ax² + bx + c = 0
• Quadratic Formula:
  `x=(-b\pm√(b^2-4ac) )/(2a)`

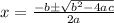
Algebra II

• Imaginary Numbers: √-1 = i

Explanation:

Step 1: Define

-4x² = 5x + 9

Step 2: Rewrite

Find standard form.

1. Subtract 5x on both sides: -4x² - 5x = 9
2. Subtract 9 on both sides: -4x² - 5x - 9 = 0

Step 3: Identify Variables

a = -4

b = -5

c = -9

Step 4: Solve for x

1. Substitute [QF]:
   `x=(5\pm√((-5)^2-4(-4)(-9)) )/(2(-4))`
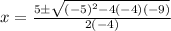
2. Exponents:
   `x=(5\pm√(25-4(-4)(-9)) )/(2(-4))`
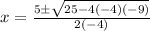
3. Multiply:
   `x=(5\pm√(25-144) )/(-8)`
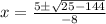
4. Subtract:
   `x=(5\pm√(-119) )/(-8)`
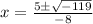
5. Factor:
   `x=(5\pm√(-1) √(119) )/(-8)`
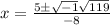
6. Simplify:
   `x=(5\pm i√(119) )/(-8)`

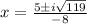
Here we see that we get imaginary numbers.

∴ the quadratic would have no real roots.