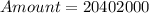Question

DU

W
tyujton of the line RS.
(4 marks)
4
Express 0.84554... as a friction in its simplest form,
(04 marks)
5. The coordinates of points A and B are ( 5, 3) and (1,9) respectively,
Find the
a) Mid point of AB
b) Length of AB
6.
1,The function is defined as tx -3x - 2x, Determine the range if the domain is (0,1,2,3)
(04 marks)

2, An open cylinder has a height of 15 cm and a radius of 7cm, calculate the surface area of the cylinder
(04 marks)

3. Given that a = (
and b = 3a, find la + bl.
(04 marks)

9. Apili has shs 20,000,000 on her fixed deposit account in a bank. The bank gives a compound interest
at a rate of 1% per annum Calculate the amount Apili will receive alter 2 years​

Answer 1

See Explanation

Step-by-step explanation:

Solving (4): 0.84554 as a fraction

The above number is to 5 decimal places, so the fraction equivalent is:

`Fraction = (84554)/(100000)`

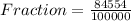
Divide numerator and denominator by 2

`Fraction = (84554/2)/(100000/2)`

`Fraction = (42277)/(50000)`

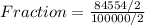
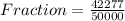
Solving (5):

`A = (5,3)`
`B = (1,9)`

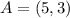
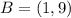
The midpoint, M is calculated as follows:

`M = ((x_1+x_2)/(2),(y_1+y_2)/(2))`

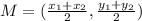
Where

`(x_1,y_1) = (5,3)`
`(x_2,y_2) = (1,9)`

`M = ((5+1)/(2),(3+9)/(2))`

`M = ((6)/(2),(12)/(2))`

`M = (3,6)`

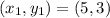
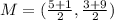
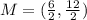
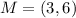
The distance, D is calculated using:

`D = √((x_1 - x_2)^2+(y_1 - y_2)^2)`

`D = √((5 - 1)^2+(3 - 9)^2)`

`D = √((4)^2+(-6)^2)`

`D = √(16+36)`

`D = √(52)`

`D = 7.21`

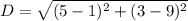
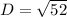
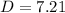
Solving (1): The expression for f(x) is not clear. So, I'll make use of:

`f(x) = 3x^2 -2x`

`Domain = \{0,1,2,3\}`

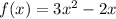
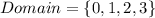
Substitute each value of the domain in
`f(x) = 3x^2 -2x`

`f(0) = 3(0)^2 - 2(0) = 0 - 0 = 0`

`f(1) = 3(1)^2 - 2(1) = 3 - 2 = 1`

`f(2) = 3(2)^2 - 2(2) = 12 - 4 = 8`

`f(3) = 3(3)^2 - 2(3) = 27 - 6 = 21`

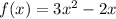
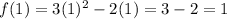
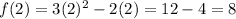
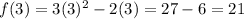
The range is:

`Range = \{0,1,8,21\}`

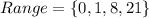
Solving (2):

`Height (H) = 15cm`
`Radius(R) = 7cm`

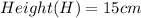
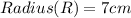
Shape: Open Cylinder

The surface area is calculated as:

`Area = 2\pi rh+ \pi r^2`

`Area = 2 * 3.14 * 7 * 15 + 3.14 * 7^2`

`Area = 659.4 + 153.86`

`Area = 813.26`

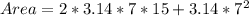
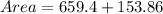
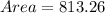
Solving (3):

The value of a is not clear. So, I'll assume that a is a

Given that

`b = 3a`

Find
`|a+b|`

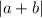
Substitute 3a for b

`|a + b| = |a + 3a|`

`|a + b| = |4a|`

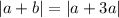
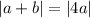
Absolute value of 4a is 4a. So,

`|a + b| = 4a`

Solving (9):

Given

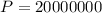`P= 20000000` --- Principal

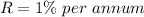`R = 1\%\ per\ annum` --- Rate

`n = 2` --- Time in years

The amount (A) is calculated as follows:

`A = P* (1 + (R)/(100))^n`

`A = 20000000 * (1 + (1)/(100))\²`

`A = 20000000 * (101/100)^2`

`A = 20000000 * 1.0201`

`A = 20402000`

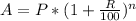
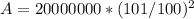
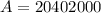
Hence, the amount at the end of 2 years is:

`Amount = 20402000`