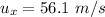Answer:
The value is
Step-by-step explanation:
From the question we are told that
The horizontal distance traveled is
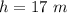
The decrease in height is
Considering the vertical velocity
Generally from kinematic equation we have that
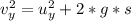
Here the initial vertical (
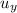 ) velocity is zero
) velocity is zero
=>
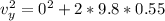
=>
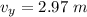
Generally the time to drop to this height is mathematically represented as

=>
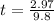
=>
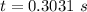
Generally given that time taken to drop to the obtained height is equal to the time taken to reach the horizontal distance , then
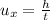
Here
 is the initial horizontal velocity
is the initial horizontal velocity
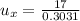
=>