Answer:
The value of k ⇨
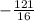
Step-by-step explanation:
⟺ Substitute a = 4 and b = -7 in the equation.
From
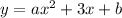
Our new equation is

⟺ Use the formula of finding k value.
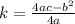
⟺ Substitute a = 4 b = 3 and c = -7 in the formula. (Arranged Expression)

If you are curious where k-value/term comes form, it comes from this equation.
