Question

If X > 0, what is one possible solution to this equation x^3 (x^2-5) = -4x

Answer 1

`x {}^(3) ( {x}^(2) - 5) = - 4x`

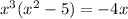
distribute x³ :

`x {}^(5) - 5 {x}^(3) = - 4x`

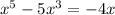
move variable to the left-hand side:

`{x}^(5) - 5 {x}^(3) + 4x = 0`

factorize out x :

`x( {x}^(4) - 5 {x}^(2) + 4) = 0`

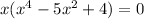
write -5x as difference:

`x( {x}^(4) - {x}^(2) - 4 {x}^(2) + 4) = 0`

factorize x² from the equation:

`x( {x}^(2) ( {x}^(2) - 1) - 4 {x}^(2) + 4) = 0`

factorize -4 from the equation:

`x( {x}^(2) ( {x}^(2) - 1) - 4( {x}^(2) - 1) = 0`

factorize (x²-1) from the equation:

`x( {x}^(2) - 1)( {x}^(2) - 4) = 0`

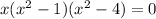
products:

1) x = 0

*ignore this as your question wants x>0

2) x²-1 = 0

x² = 1

x = √1

x=1

3) x²-4 = 0

x² = 4

x = √4

x=2

thus, x=1, x=2