Question

g A rotating wheel requires 5.00 s to rotate 28.0 revolutions. Its angular velocity at the end of the 5.00-s interval is 96.0 rad/s. What is the constant angular acceleration (in rad/s) of the wheel

Answer 1

The angular acceleration of the wheel is 15.21 rad/s².

Step-by-step explanation:

Given that,

Time = 5 sec

Final angular velocity = 96.0 rad/s

Angular displacement = 28.0 rev = 175.84 rad

Let
`\alpha` be the angular acceleration

We need to calculate the angular acceleration

Using equation of motion

`\theta=\omega_(i) t+(1)/(2)\alpha t^2`

Put the value in the equation

`175.84=\omega_(i)* 5+(1)/(2)*\alpha*(5)^2`

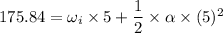
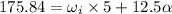`175.84=\omega_(i)* 5+12.5\alpha`......(I)

Again using equation of motion

`\omega_(f)=\omega_(i)+\alpha t`

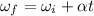
Put the value in the equation

`96.0=\omega_(i)+\alpha * 5`

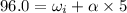
On multiply by 5 in both sides

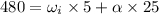`480=\omega_(i)* 5+\alpha* 25`....(II)

On subtract equation (I) from equation (II)

`480-175.84=\alpha(25-5)`

`304.16=\alpha*20`

`\alpha=(304.16)/(20)`

`\alpha=15.21\ rad/s^2`

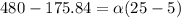
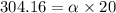
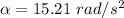
Hence, The angular acceleration of the wheel is 15.21 rad/s².