Answer:
The average rate of change
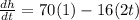
At t = 1
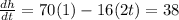
at t=3
Explanation:
Step(I):-
The given function h(t) = 3+70t - 16t²
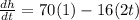
The
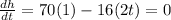
70 - 32 t = 0
⇒ 70 = 32 t
⇒
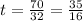
Step(ii):-
The average rate of change in h(t) between t = 1 second and t = 3 second
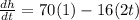
At t = 1
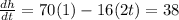
At t = 3