Question

Total no of whole number of that have less than 1000 and divisble by 7​

Answer 1

There are 142 whole numbers less than 1000 and divisible by 7.

Explanation:

The multiples of 7 form an arithmetic sequence like shown:

7, 14, 21, ...

The last term of this sequence can be found by dividing 1000/7=142.9 and rounding down to the previous integer: 142*7= 994.

Thus, the sequence has:

a1=7, r=7, an=994. We need to find n and we'll do that by using the general term formula:

`a_n=a_1+(n-1).r`

And solving for n:

`\displaystyle n= (a_n-a_1)/(r)+1`

`\displaystyle n= (994-7)/(7)+1`

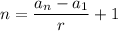
n = 142

There are 142 whole numbers less than 1000 and divisible by 7.