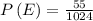Question

A fair coin is flipped twelve times. What is the probability of the coin landing tails up exactly nine times?

Answer 1

`P\left(E\right)=(55)/(1024)`

Explanation:

Given that a fair coin is flipped twelve times.

It means the number of possible sequences of heads and tails would be:

2¹² = 4096

We can determine the number of ways that such a sequence could contain exactly 9 tails is the number of ways of choosing 9 out of 12, using the formula

`nCr=(n!)/(r!\left(n-r\right)!)`

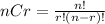
Plug in n = 12 and r = 9

`=(12!)/(9!\left(12-9\right)!)`

`=(12!)/(9!\cdot \:3!)`

`=(12\cdot \:11\cdot \:10)/(3!)` ∵
`(12!)/(9!)=12\cdot \:11\cdot \:10`

`=(1320)/(6)` ∵
`3!\:=\:3* 2* 1=6`

`=220`

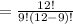
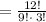
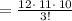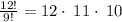
Thus, the probability will be:

`P\left(E\right)=(n\left(E\right))/(n\left(S\right))`

`=(220)/(4096)`

`=(55)/(1024)`

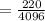
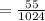
Thus, the probability of the coin landing tails up exactly nine times will be:

`P\left(E\right)=(55)/(1024)`