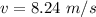Question

g What is the final velocity of a hoop that rolls without slipping down a 6.92 m high hill, starting from rest

Answer 1

The value is
`v = 8.24 \ m/s`

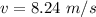
Step-by-step explanation:

From the question we are told that

The height of the hill is
`h = 6.92 \ m`

Generally from the law of energy conservation we have that

`PE = KE + RKE`

Here PE is the potential energy of the hoop which is mathematically represented as

`PE = mgh`

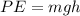
KE is the kinetic energy of the hoop which is mathematically represented as

`KE = (1)/(2) * m * v^2`

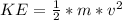
And

RKE is the rotational kinetic energy which is mathematically represented as

`RKE = (1)/(2) * I * w^2`

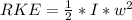
Here I is the moment of inertia of the hoop which is mathematically represented as

`I = m * r^2`

and w is the angular velocity which is mathematically represented as

`w = (v)/(r)`

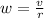
So

`RKE = (1)/(2) * m r^2 * (v)/(r) ^2`

=>
`RKE = (1)/(2) * m r * v^2`

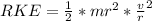
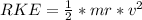
So

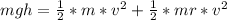
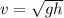
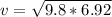
`mgh = (1)/(2) * m * v^2 + (1)/(2) * m r * v^2`

=>
`v = √(gh)`

=>
`v = √(9.8 * 6.92 )`

=>
`v = 8.24 \ m/s`