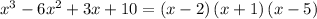Question

Use the x-intercept method to find all real solutions of the equation.x^3-6x^2+3x+10=0

Answer 1

Please check the explanation.

Explanation:

Given the equation

`x^3-6x^2+3x+10=0`

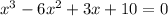
Step 1:

Writing the equation

`x^3-6x^2+3x+10=0`

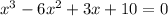
Step 2:

In order to determine the x-intercept, we need to plot the graph.

All the values at y = 0 would be x-intercepts of the equation.

Please check the attached graph below.

Step 3:

It is clear from the graph, the points where y = 0, the x-values are: -1, 2 and 5.

Hence, (-1, 0) (2, 0) and (5, 0) are the x-intercepts of the equation.

Thus, x = -1, x = 2, and x = 5 are the solution of the equation.

Hence,

`x^3-6x^2+3x+10=\left(x-2\right)\left(x+1\right)\left(x-5\right)`