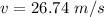Complete Question
The complete question is shown on the first uploaded image
Answer:
a
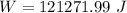
b
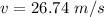
Step-by-step explanation:
From the question we are said that
The mass of the shed is
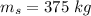
The pulling force is
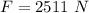
The angle is
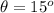
The distance covered is

The kinetic force is

Generally the work done is mathematically represented as
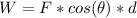
=>
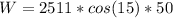
=>
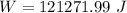
Generally according to the work-energy theorem
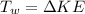
Here
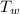 is total work done which is mathematically represented as
is total work done which is mathematically represented as
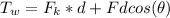
=>

=>
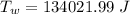
Also
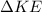 is the change in kinetic energy which is mathematically represented as
is the change in kinetic energy which is mathematically represented as
![\Delta KE = (1)/(2) * m * [ v^2 - u^0 ]](https://img.qammunity.org/2021/formulas/physics/college/m74bws4g1znfkg0ztdk37phexqlh93o7j9.png)
Here u is the initial velocity of the shed when at rest
![\Delta KE = (1)/(2) * 375 * [ v^2 - 0^0 ]](https://img.qammunity.org/2021/formulas/physics/college/dxsoxvabyt8936l8e6y6k2klz2pkq545a4.png)
=>
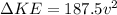
So
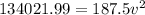
=>
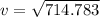
=>