Question

Determine whether each function is even, odd, or neither.

f(x) = Vr²9

g(x) = |x-31

f(x) =

g(x) = x + x2

Answer 1

Please check the explanation.

Explanation:

Even Functions:

The function is unchanged when it is reflected about the y-axis.

i.e.

f(-x) = f(x)

Odd Functions:

The function is unchanged when it is rotated 180° about the origin.

i.e.

f(-x) = -f(x)

Neither Functions:

f(-x) ≠ -f(x)

Let us check the given functions:

• f(x) = Vx²9

plug –x in for x

f(-x) = V(-x)²9

f(-x) = Vx²9

f(-x) = f(x)

Therefore, the function f(x) = Vx²9 is even function.

• g(x) = |x-3|

plug –x in for x

as

`f\left(-x\right)=|x+3|`

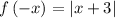
and

`-f\left(x\right)=-\left|x-3\right|`

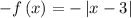
so

f(-x) ≠ f(x)

f(-x) ≠ -f(x)

Thus,

g(x) = |x-3| is neither an even nor an odd function.

• g(x) = x + x²

plug –x in for x

g(-x) = (-x) + (-x)²

g(-x) = -x + x²

g(-x) = -(x-x²)

so

f(-x) ≠ f(x)

f(-x) ≠ -f(x)

Thus, it is neither an even nor an odd function.

Thus,

g(x) = x + x² is neither an even nor an odd function.