Question

(a) What is the magnitude of the tangential acceleration of a bug on the rim of a 13.0-in.-diameter disk if the disk accelerates uniformly from rest to an angular speed of 79.0 rev/min in 4.40 s

Answer 1

An angular speed of 79.0 rev/min = 4740 rev/s corresponds to a tangential speed of

(4740 rev/s) • (2π (13.0 in) / rev) = 123,240π in/s ≈ 387,000 in/s

and thus a tangential acceleration of

(123,240π in/s - 0) / (4.40 s) = 28,009.1π in/s² ≈ 88,000 in/s²

Answer 2

The magnitude of the tangential acceleration of the bug is 12.22 in/s²

Step-by-step explanation:

Given;

diameter of the disk, d = 13.0 in

radius of the disk, r = d/2 = 6.5 in

initial angular speed of the disk,
`\omega _i` = 0

final angular speed of the disk,
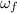`\omega _f` = 79 re/min

=
`(79 \ rev)/(\min) * (2\pi)/(rev) * (1\min)/(60s) = 8.274 \ rad/s`

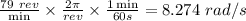
time of motion, t = 4.40 s

The angular acceleration is calculated as;

`\alpha = (\omega _f -\omega _i)/(t)`

`\alpha = (8.274 -0)/(4.4) \\\\\alpha = 1.88 \ rad/s^2`

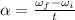
The tangential acceleration is calculated as;

`a_t = \alpha r\\\\a_t = (1.88 \ rad/s^2)(6.5 \ in)\\\\a_t = 12.22 \ in/s^2`

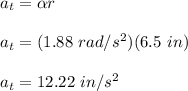
Therefore, the magnitude of the tangential acceleration of the bug is 12.22 in/s²