Answer:
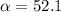
Step-by-step explanation:
Given
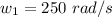 --- initial angular velocity
--- initial angular velocity
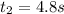 -- Initial time
-- Initial time
Because the engine completely stops, we have the following:
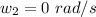 --- final angular velocity
--- final angular velocity
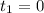 --- final time
--- final time
Required:
Determine the angular acceleration (
 )
)
The angular is calculated as thus:
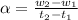
i.e. the ratio of change in angular velocity to change in time
Substitute in the required values, the expression becomes:


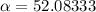
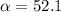 -- approximated
-- approximated
Hence, the engine's angular acceleration is 52.1rad/s^2