Question

You push a manual lawn mower across the lawn at constant speed. What is the value of the coefficient of friction between the mower and the grass

Answer 1

0.27

Step-by-step explanation:

The question is incomplete. Here is the complete question:

You are pushing a 13.3 kg lawn mower across the lawn with a force of 200 N. What is the value of the coefficient of friction between the mower and the grass if the mower moves with a constant velocity? The force is applied downward at an angle of 65° with the horizontal.

According to Newton's second law of motion:

`\sum F_x= ma_x\\F_(app) - F_f = ma_x\\`

`F_f = \mu R\\`

`F_(app) - \mu Rcos \theta = ma_x`

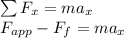
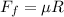
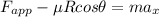
Fapp is the applied force = 200N

Ff is the frictional force

`\mu` is the coefficient of friction between the mower and the grass

R is the reaction

m is the mass of the object

ax is the acceleration

Given

R = mg = 13.3*9.8

R = 130.34N

m = 13.3kg

ax = 0m/s² (constant velocity)

Fapp = 200N

`\theta = 65^0`

Substitute the given parameters into the formula and get the coefficient of friction as shown;

Recall that:
`F_f = \mu R\\`

`\mu = (F_f)/(R)\\\mu = (F_(x)cos65)/(F_y+W) \\\mu =( 200cos65)/(200sin65+13.3(9.8))\\\mu = (84.52)/(181.26+130.34)\\\mu = (84.52)/(311.6)\\\mu = 0.27`

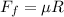
Hence the coefficient of friction between the mower and the grass is 0.27