Question

g If the car has a mass of 124 g and it reaches a maximum vertical height of 1.40 m above the floor, what was the speed of the car while it was moving along the floor

Answer 1

The car was moving at a speed of approximately 5.240 meters per second along the floor.

Step-by-step explanation:

Let suppose that the car represents a conservative system, that is, that all non-conservative forces (i.e. friction, air viscosity) can be neglected. The initial speed of the vehicle can be determined by means of the Principle of Energy Conservation, which states that:

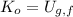`K_(o) = U_(g,f)` (1)

Where:

`K_(o)` - Initial translational kinetic energy, measured in joules.

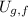`U_(g,f)` - Final gravitational potential energy, measured in joules.

By definitions of translational kinetic energy and gravitational potential energy, we expand the equation above:

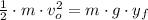`(1)/(2)\cdot m \cdot v_(o)^(2) = m\cdot g \cdot y_(f)` (2)

Where:

`m` - Mass, measured in kilograms.

`g` - Gravitational acceleration, measured in meters per square second.

`v_(o)` - Initial speed of the car, measured in meters per second.

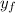`y_(f)` - Final vertical height of the car, measured in meters.

If we know that
`m = 0.124\,kg`,
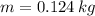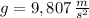`g = 9,807\,(m)/(s^(2))` and
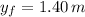`y_(f) = 1.40\,m`, then the initial speed of the car is:

`v_(o) = \sqrt{2\cdot g \cdot y_(f)}`

`v_(o) = \sqrt{2\cdot \left(9.807\,(m)/(s^(2)) \right)\cdot (1.40\,m)}`

`v_(o) \approx 5.240\,(m)/(s)`

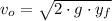
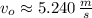
The car was moving at a speed of approximately 5.240 meters per second along the floor.