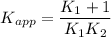The question is incomplete. The complete question is :
In the native state, myokinase exists in two distinct conformations (MK1 and MK2). It unfolds to the unfolded state (MKU) only from MK2.
K1 K2
MK1 ⇄ MK2 ⇄ MKU
Derive the expression for the apparent equilibrium constant (Kapp) for the folding of MKU in terms of K1 and K2, where Kapp = ( [MK1] + MK2] ) / [MKU].
Solution :
Derive the expression for the apparent equilibrium constant
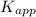 :
:
![$K_(app) = ([MK_1]+[MK_2])/(MKU)$](https://img.qammunity.org/2021/formulas/physics/college/t17nkhijc5idhuz98qghwbr4p6rg1q3p7b.png) ............(i)
............(i)
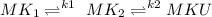
![$K_1 = ([MK_2])/([MK_1]) \ \text{ and} \ K_2 = ([MKU])/([MK_2])$](https://img.qammunity.org/2021/formulas/physics/college/mef8cjqnqrtbe7r6rmw4ov0kwdadbbmcjv.png)
![$K_(app) = ([MK_1]+[MK_2])/(MKU)$](https://img.qammunity.org/2021/formulas/physics/college/t17nkhijc5idhuz98qghwbr4p6rg1q3p7b.png)
Divide by
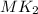 in both numerator and the denominator.
in both numerator and the denominator.
![$K_(app)= (([MK_1])/([MK_2])+1)/(([MKU])/([MK_2]))$](https://img.qammunity.org/2021/formulas/physics/college/ebkal4hxref7gbrtnv2504uq8jvigwcfgt.png) ................(ii)
................(ii)
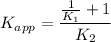
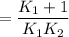
Therefore the required expression is :