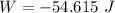Answer:
The value is
Step-by-step explanation:
From the question we are told that
The mass of the block is

The force is
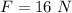
The angle is
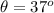
The first speed of the block is
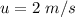
The second speed of the block is
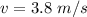
The displacement is

Gnerally from kinematic equation we have that
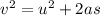
=>
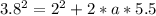
=>

Generally the net force acting on the crate is mathematically represented as
![F_(net) = [ F cos (\theta ) - F_f ] = ma](https://img.qammunity.org/2021/formulas/physics/high-school/w8n3h7we3xhdix3e8vauwm4390vjp3ncuk.png)
Here
 is the frictional force acting on the crate
is the frictional force acting on the crate
So
![[ 16 cos (37 ) - F_f ] = 3 * 0.9491](https://img.qammunity.org/2021/formulas/physics/high-school/7znsldelaxtyrnuhq0vgs5zvwsk26aqr00.png)
=>
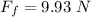
Generally the work done by friction during the displacement is mathematically represented as
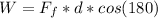
=>
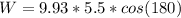
=>