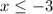Question

Type the correct answer 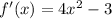in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s).

Find the inverse of the given function.

f() = -kvo + 3, < > -3

Answer 1

`f'(x) = 4x^2 - 3` for
`x \le -3`

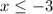
Explanation:

See attachment for proper question

Given

`f(x) = -(1)/(2)√(x + 3)`

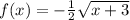
For

`x \ge -3`

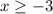
Required

Determine the inverse function

`f(x) = -(1)/(2)√(x + 3)`

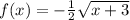
Replace f(x) with y

`y = -(1)/(2)√(x + 3)`

Swap the positions of x and y

`x = -(1)/(2)√(y + 3)`

Multiply both sides by -2

`-2 * x =-2 * -(1)/(2)√(y + 3)`

`-2x =√(y + 3)`

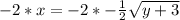
Square both sides

`(-2x)^2 =(√(y + 3))^2`

`4x^2 =y + 3`

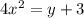
Make y the subject

`y = 4x^2 - 3`

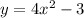
The inverse has been solved. So, we need to replace y with f'(x)

`f'(x) = 4x^2 - 3`

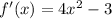
Next, is to determine the interval

`x \ge -3`

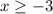
Change inequality to
`\le`

`x \le -3`

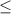
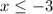
Hence, the inverse function is:

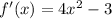`f'(x) = 4x^2 - 3` for
`x \le -3`