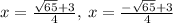Question

the equation is -2x² = 4-3 (x + 1) and the question is justify that it is a 2nd degree equation with the unknown x complete.

Answer 1

Please check the explanation.

Explanation:

Given the equation

-2x² = 4-3 (x + 1)

-2x² = 4-3x-3

-2x² = -3x -7

0 = 2x² -3x -7

We know that the degree of the equation is the highest power of x variable in the given equation.

In the equation 0 = 2x² -3x -7 the highest power of x variable in the given equation is 2.

Thus, the degree of the equation is 2.

Also in the equation 0 = 2x² -3x -7, the unknown variable is 'x'.

Let us determine the value 'x'

2x² -3x -7 = 0

Add 7 to both sides

`2x^2-3x-7+7=0+7`

`2x^2-3x=7`

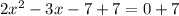
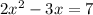
Divide both sides by 2

`(2x^2-3x)/(2)=(7)/(2)`

`x^2-(3x)/(2)=(7)/(2)`

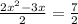
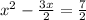
Add (-3/4)² to both sides

`x^2-(3x)/(2)+\left(-(3)/(4)\right)^2=(7)/(2)+\left(-(3)/(4)\right)^2`

`x^2-(3x)/(2)+\left(-(3)/(4)\right)^2=(65)/(16)`

`\left(x-(3)/(4)\right)^2=(65)/(16)`

`\mathrm{For\:}f^2\left(x\right)=a\mathrm{\:the\:solutions\:are\:}f\left(x\right)=√(a),\:-√(a)`

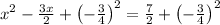
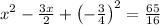
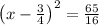
solving

`x-(3)/(4)=\sqrt{(65)/(16)}`

`x-(3)/(4)=(√(65))/(√(16))`

`x-(3)/(4)=(√(65))/(4)`

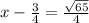
Add 3/4 to both sides

`x-(3)/(4)+(3)/(4)=(√(65))/(4)+(3)/(4)`

`x=(√(65)+3)/(4)`

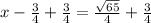
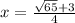
similarly solving

`x-(3)/(4)=-\sqrt{(65)/(16)}`

`x=(-√(65)+3)/(4)`

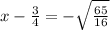
So the solution of the equation will have the values of x such as:

`x=(√(65)+3)/(4),\:x=(-√(65)+3)/(4)`