Answer:
x = 53
y = 30
Explanation:
Step(I):-
Given equations are
x -2y =-7 ...(I)
5x-9y =-5 ..(ii)
The matrix form AX = B
![\left[\begin{array}{ccc}1&-2\\ 5 & -9\\\end{array}\right] \left[\begin{array}{ccc}x\\y\\\end{array}\right] = \left[\begin{array}{ccc}-7\\-5\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ongg6x1he81ko8rnf7szq687kp95q4yj4y.png)
The determinant
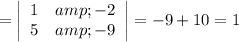
By using Cramer's Rule
Δ₁ =
![\left[\begin{array}{ccc}-7&-2\\\\-5&-9\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/urlgdklwxtpk9utwot3m8dbqi2kxkfauw7.png)
The determinant is Δ₁ = -9 X -7 - (10 ) = 53
x = Δ₁ / Δ
x = 53
The determinant
Δ₂ =
Δ₂ = -5 +35
y = Δ₂/Δ = 30