Answer:
4 units
Explanation:
Given
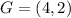
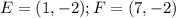
Required
Determine the distance
We need to calculate the equation of EF
But first, we calculate the slope (m)

Where


So:
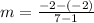
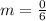
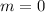
The equation is then calculated as:

Where
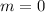 and
and

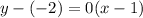
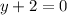
So, we are to calculate the distance between point
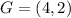 and line
and line
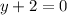
The distance is calculated using:
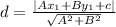
In
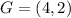 , we have:
, we have:
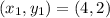
A general equation has
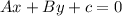 as its format
as its format
By comparison
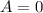
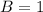
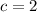
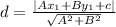 becomes
becomes
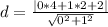
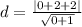
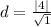


Hence, the distance is 4 units