Question

Prove that tan 10+tan 70'+taniou = tanio tanfo'tam 1oo.​

Answer 1

Question:

Prove that:

`tan(10) + tan(70) + tan(100) = tan(10). tan(70). tan(100)`

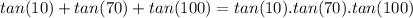
Answer:

Proved

Explanation:

Given

`tan(10) + tan(70) + tan(100) = tan(10). tan(70). tan(100)`

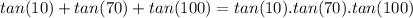
Required

Prove

`tan(10) + tan(70) + tan(100) = tan(10). tan(70). tan(100)`

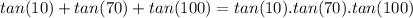
Subtract tan(10) from both sides

`- tan(10)+tan(10) + tan(70) + tan(100) = tan(10). tan(70). tan(100) - tan(10)`

`tan(70) + tan(100) = tan(10). tan(70). tan(100) - tan(10)`

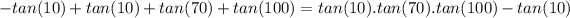
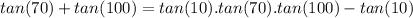
Factorize the right hand size

`tan(70) + tan(100) = -tan(10)(-tan(70). tan(100) + 1)`

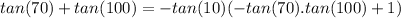
Rewrite as:

`tan(70) + tan(100) = -tan(10)(1-tan(70). tan(100))`

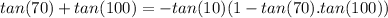
Divide both sides by
`1-tan(70). tan(100)`

`(tan(70) + tan(100))/(1-tan(70). tan(100)) = (-tan(10)(1-tan(70). tan(100)))/(1-tan(70). tan(100)))`

`(tan(70) + tan(100))/(1-tan(70). tan(100)) = -tan(10)`

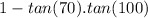
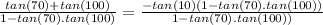
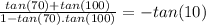
In trigonometry:

`tan(A + B) = (tan(A) + tan(B))/(1 - tan(A)tan(B))`

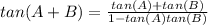
So:

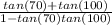`(tan(70) + tan(100))/(1 - tan(70)tan(100))` can be expressed as:
`tan(70 + 100)`

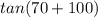
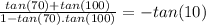`(tan(70) + tan(100))/(1-tan(70). tan(100)) = -tan(10)` gives

`tan(70 + 100) = -tan(10)`

`tan(170) = -tan(10)`

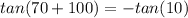
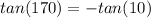
In trigonometry:

`tan(180 - \theta) = -tan(\theta)`

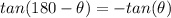
So:

`tan(180 - 10) = -tan(10)`

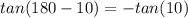
Because RHS = LHS

Then:

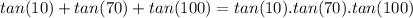`tan(10) + tan(70) + tan(100) = tan(10). tan(70). tan(100)` has been proven