Question

A point P on the unit radius circle centred at the origin has coordinates (5/13, 12/13).

Which one of the following is the angle between the positive x-axis and the line segment
joining the origin to P

Answer 1

θ=67.38°

Explanation:

Unit Circle

It's a circle with radius 1 where all the trigonometric functions are defined.

In the figure below the segment from the center to the point P forms an angle θ whose coordinates x and y are defined as:

x = cos θ

y = sin θ

We are given both coordinates (5/13,12/13). They should correspond to the same angle. Solving for θ:

`\theta=\arccos (5/13)`

`\theta=67.38^\circ`

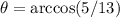
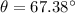
And also:

`\theta=\arcsin (12/13)`

`\theta=67.38^\circ`

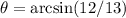
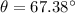
The coordinates correspond to the same angle, thus θ=67.38°