Answer:
The side length of the rhombus is 25 cm
Explanation:
Rhombus
We know that the diagonals of a rhombus are perpendicular to each other.
We are given the length of each diagonal as d1=30 cm and c2=40 cm.
They meet at the center at half those lengths, thus a right triangle is formed with legs 30/2=15 cm and 40/2=20 cm
Thus, applying Pythagora's Theorem, the side length of the rhombus is:
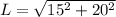

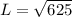
L = 25 cm
The side length of the rhombus is 25 cm