Question

Help ppls thank u guys <3

Answer 1

The magnitude of the sum of the two vectors is approximately 169.34 m

Step-by-step explanation:

The given vectors are;

Vector B;

Magnitude = 101 m

Direction = 60.0° (30.0° west of north)

Resolving the vector into its x and y component vectors gives;

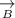`\underset{B}{\rightarrow}` = 101 × cos(60.0°)·i + 101 × sin(60.0°)·j = 55·i + 55·√3·j

∴
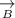`\underset{B}{\rightarrow}` = 55·i + 55·√3·j

Vector A;

Magnitude = 85.0 m

Direction = West

Resolving the vector into its x and y component vectors gives;

`\underset{A}{\rightarrow}` = 85.0 × cos(0.0°)·i + 85.0 × sin(0.0°)·j = 85.0·i + 0·j

∴
`\underset{A}{\rightarrow}` = 85.0·i

The sum of the two vectors is
`\underset{B}{\rightarrow}` +
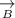`\underset{A}{\rightarrow}` = 55·i + 55·√3·j + 85.0·i = 140.0·i + 55·√3·j

The direction of the sum of the two vectors, θ = arctan(y-component of the vector)/(x-component of the vector))

Therefore, θ = arctan((55·√3)/140) ≈ 34.23° north of west or 55.77° west of north

The magnitude of the sum of the two vectors, R is R = √(140² + (55·√3)²) ≈ 169.34 m.