Question

In a class of so students, 35 like to play cricket

25 like to play to football, also each student likes
to play at least one of the two games. How many
students like to play both the games? Represent the given information in a venn diagram
​

Answer 1

10

Explanation:

Given that:

Total number of students = 50

Students who like to play football = 25

`n(A) = 25`

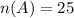
Students who like to play cricket = 35

`n(B) = 35`

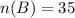
Each student likes to play at least one game.

It means the universal set is equal to the union of the above two sets.

`n(U) =n(A\cup B) = 50`

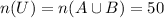
To find:

The number of students who play both the games and representation of the given situation in the form of a Venn diagram.

i.e.
`n(A\cap B) = ?`

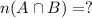
Solution:

First of all, let us have a look at the formula for the number of elements in the union of two sets.

`n(A\cup B)=n(A)+n(B)-n(A\cap B)`

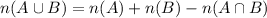
Putting the values in the formula, we need to find the value of
`n(A\cap B)`

`50=25+35-n(A\cap B)\\\Rightarrow 50-60=-n(A\cap B)\\\Rightarrow n(A\cap B)=\bold{10}`

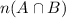
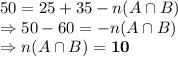
Therefore, the number of students who like to play both the games is 10.