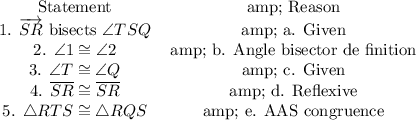Answer:
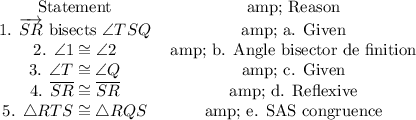
Explanation:
Here we are given two triangles namely
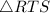 and
and
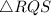 .
.
Given that:
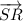 bisects
bisects
 .
.
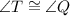
To prove:
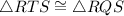 by using a 2 column proof.
by using a 2 column proof.
Solution:
First of all, let us have a look at the meaning of two column proof.
A two column proof is written in the form of a table which has two columns.
One column contains Statement and the second column contains the reason of the statement.
Let us have a look at the second statement.
By definition of Angle bisectors, we can say the two angles are congruent.
4th statement's reason is that the two sides are the same side i.e. reflexive.
5th statement is true because of the reason AAS (Angle Angle Side) congruence.